Существует два метода получения случайных величин с заданным законом распределения из равномерно распределенных на интервале [0,1) случайных чисел - с помощью аналитических преобразований или с использованием табличных преобразований. Рассмотрим эти методы.
Метод аналитического преобразования случайных величин
Большинство способов этого метода преобразования основано на использовании последовательности равномерно распределенных в интервале
(0, 1) случайных чисел {xi}. В математической статистике доказывается теорема: если случайная величина
Х имеет плотность распределения
f(х), то распределение случайной величины Y=F(x) является равномерным в интервале
(0,1). Здесь под
F(x) понимается функция распределения случайной величины
Х. Следовательно, можно поступить наоборот: построив функцию распределения
F(x), выбирает случайное число Y из равномерного распределения в интервале
(0,1) и определяет то значение аргумента х , для которого
F(x) = Y. Полученная таким образом случайная величина
Х будет иметь заданную функцию распределения
F(x).
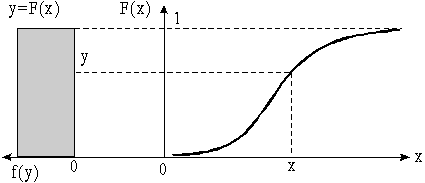
Эта же задача может быть решена не только графическими построениями, но и рядом других способов. В частности, аналитический способ основан на обратном преобразовании
x = F -1(y), где F -1 - функция, обратная функции
F. Это преобразование сводится к решению интегрального уравнения относительно
хi.
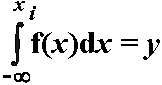
т.е. определяется такое значение xi, при котором функция распределения равна
y.
Экспоненциальное распределение.
Чтобы получить случайное число xi, распределенное по экспоненциальному закону, необходимо решить уравнение
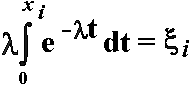
После интегрирования получим
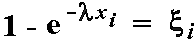
Решая относительно xi и учитывая, что распределение
(1-xi) и xi эквивалентны, будем иметь
xi =- 1/ λ*ln xi
Нормальное распределение.
Функция плотности вероятностей нормального закона распределения имеет вид:
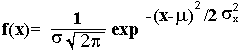
где: математическое ожидание Mx = m; дисперсия
Dx = S2x
Для имитации нормально распределенных случайных величин используется следующее преобразование:
x= Mx + u * Sx ,
где u имеет плотность вероятностей
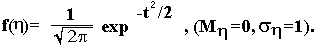
Для получения случайных чисел, подчиненных нормальному закону распределения, можно воспользоваться
центральной предельной теоремой теории вероятностей (теоремой Ляпунова). Сущность теоремы состоит в том, что закон распределения суммы
m независимых случайных величин, имеющих один и тот же закон распределения, при неограниченном увеличении числа слагаемых m приближается к нормальному.
В общем случае сумма m равномерно распределенных в интервале
(a,b) независимых случайных величин стремиться к нормальному распределению с математическим ожиданием M(x)=m*(a+b)/2 и дисперсией
S2x = m*(a+b)2/12.
Если использовать распределение со значениями
a=0; b=1, то суммарное распределение будет иметь следующие параметры:
M(x)=m/2 и дисперсией S2x = m/12.
Пусть имеет плотность вероятностей (1). Тогда, согласно центральной предельной теореме, располагая последовательностью равномерно распределенных в интервале (0,1) случайных чисел
xi , получим:
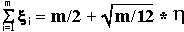
Отсюда
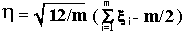
Тогда подставив в (1), получим:
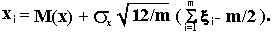
В зависимости от требуемой точности число слагаемых может изменяться в пределах от 5 до 15. Принимая m=12, получим:
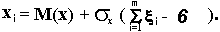
Метод табличного преобразования случайных величин
Этот метод заключается в том , что используется таблица накопленных или относительных частот желаемого распределения. Например, предположим, что случайная величина должна получать значения 2, 5, 8, 9 и 12 с относительной частотой 0,15; 0,20; 0,25; 0,22 и 0,18 соответственно. Эта данные приведены в таблице.
| Значение случайной величины | Относительная частота | Накопленная частота | Диапазон | Интервал |
| 2 | 0,15 | 0,15 | 0,0÷0,15 | 1 |
| 5 | 0,20 | 0,35 | 0,15+÷0,35 | 2 |
| 8 | 0,25 | 0,60 | 0,35+÷0,60 | 3 |
| 9 | 0,22 | 0,82 | 0,60+÷0,82 | 4 |
| 12 | 0,18 | 0,18 | 0,82+÷1,0 | 5 |
Предположим, что необходимо разыграть случайное число в соответствии с таблицей. Сначала разыгрывается случайная величина на интервале [0,1). Пусть этим числом будет 0,523664. Согласно таблице это число попадает в интервал 3, следовательно окончательно случайная величина равна 3.
Для непрерывной случайной величины в левом столбце вместо конкретных значений необходимо указывать интервал.