Однофакторный дисперсионный анализ применяется для проверки гипотезы о равенстве математических ожиданий нескольких генеральных совокупностей. Такого рода задачи возникают, когда необходимо выяснить оказывает ли на выходную зависимую переменную y влияние входная x, принимающая дискретные значения. Например, оказывает ли влияние на y сорт сырья (высший, I, II,.. и т.д.), можно ли считать цены конкурирующих фирм одинаковыми в статистическом смысле или подвержены ли цены сезонным изменениям и т.п. Таким образом, в этой модели входная переменная x принимает дискретные значения, а выходная переменная y является непрерывной случайной величиной, вероятностная природа которой обусловлена наличием аддитивной помехи e.
ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ БАЗИРУЕТСЯ НА СЛЕДУЮЩИХ ПРЕДПОСЫЛКАХ:
| 1.
В каждом наблюдении ei имеет нормальное распределение с нулевым МО и
конечной
дисперсией.
2. Для любого i дисперсия ei является величиной постоянной. |
Рассмотрим вычислительную процедуру однофакторного дисперсионного анализа. Пусть x принимает k различных значений или, как говорят, фактор x имеет k уровней. Пусть на каждом из уровней имеется n наблюдений выходной величины y. Тогда результаты можно представить в виде таблицы (столбцы - уровни фактора x, строки - наблюдения y).
| №№ набл. | Уровни входного фактора x | |||||
| 1 | 2 | ... | j | ... | k | |
| 1 | y11 | y12 | ... | y1j | ... | y1k |
| 2 | y21 | y22 | ... | y2j | ... | y2k |
| ... | ... | ... | ... | ... | ... | ... |
| i | yi1 | yi2 | ... | yij | ... | yik |
| ... | ... | ... | ... | ... | ... | ... |
| n | yn1 | yn2 | ... | ynj | ... | ynk |
Если уровни фактора x не оказывают влияние на математическое ожидание y, то все наблюдения представляют собой выборку из одной генеральной совокупности (при условии выполнения приведенных выше предпосылок). Тогда, дисперсию генеральной совокупности можно оценить двумя независимыми оценками: через средние значения y для каждого из уровней x или как среднее арифметическое оценок дисперсий y для каждого из уровней x. Первая оценка называется оценкой дисперсии уровней S2ур, вторая - оценкой дисперсии ошибки S2ош.
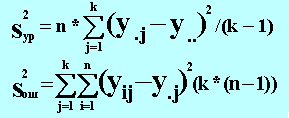
где:
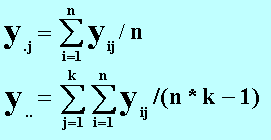
y.j - среднее по j-му уровню, y.. - общее среднее.
Если влияние уровней фактора x на математическое ожидание отсутствует, то отношение
F = S2ур/S2ош
подчинено закону распределения Фишера. Характеристики этого распределения зависят от числа степеней свободы оценок S2ур и S2ош (числа степеней свободы числителя ν1=(k-1) и знаменателя ν2=k*(n-1)). Для любого заданного уровня значимости α всегда существует критическое значение Fкр, превысить которое F при отсутствии влияния уровней x может с вероятностью не более α. Это означает, что если в результате обработки данных расчетное значение F-статистики превысит соответствующее Fкр, то данные противоречат гипотезе о равенстве математических ожиданий y для всех уровней x. Если F<Fкр, то данные не противоречат этой гипотезе, и следует считать, что уровни x не оказывают влияние на математическое ожидание y. Например, пусть фактор x имеет 4 уровня (k=4)и на каждом уровне проведено 5 наблюдений. В результате расчетов получены оценки:
S2ур=11,04; S2ош=2,5;
F=S2ур/S2ош=11,04/2,5=4,42;
пусть α=0,05.
Ниже приведен фрагмент таблицы критических значений Fкр для α=0,05. Строки таблицы - числа степеней свободы знаменателя ν2, столбцы - числителя ν1. Значение Fкр находится на пересечении столбца и строки, соответствующих числам степеней свободы. В примере (ν1=(4-1)=3,ν2=4*(5-1)=16), Fкр = 3,24, следовательно данные противоречат гипотезе о равенстве математических ожиданий. Иногда при вычислении F приводится его ЗНАЧИМОСТЬ (p-Value). Если эта величина меньше заданного α, то данные противоречат гипотезе о равенстве математических ожиданий.
| ν2 | ν1 | ||||
| ... | 2 | 3 | 4 | ... | |
| ... | ... | .... | .... | ... | ... |
| 15 | ... | 3,68 | 3,29 | 3,06 | ... |
| 16 | ... | 3,63 | 3,24 | 3,01 | ... |
| 17 | ... | 3,59 | 3,20 | 2,97 | ... |