СЛУЧАЙНЫМ СОБЫТИЕМ называется событие которое может при одних и тех же внешних условиях произойти, а может и нет. Например успешная сдача экзамена или зачета.
ВЕРОЯТНОСТЬ СЛУЧАЙНОГО СОБЫТИЯ можно рассматривать как меру неопределенности события. Эта мера принимает значения в пределах от 0 до 1. Если событие невозможно, то вероятность этого события равна 0. Если событие происходит всегда, то вероятность этого события равна 1. Иногда вероятность события задают в процентах (от 0% до 100%). Например, вероятность дождя в ясный солнечный день может быть равна 0,1 или 10%.
СЛУЧАЙНОЙ ВЕЛИЧИНОЙ называется величина, которая принимает различные значения при одних и тех же внешних условиях. Например, изменение курса валют при неизменности цен на энергоносители.
Случайные величины существуют двух видов: ДИСКРЕТНЫЕ и НЕПРЕРЫВНЫЕ. ДИСКРЕТНОЙ случайной величиной называется случайная величина, которая принимает КОНЕЧНОЕ ЧИСЛО РАЗЛИЧНЫХ ЗНАЧЕНИЙ. НЕПРЕРЫВНОЙ случайной величиной называется случайная величина, которая принимает ЛЮБОЕ ЗНАЧЕНИЕ НА НЕКОТОРОМ (возможно и бесконечном) ИНТЕРВАЛЕ.
Описание поведения случайной величины возможно в различных формах. Различают графическую, табличную, аналитическую и параметрическую формы описаний.
Графическое описание непрерывных случайных величин задается двумя видами графиков: графиком ФУНКЦИИ РАСПРЕДЕЛЕНИЯ F(X) и производной от этой функции - графиком ФУНКЦИИ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ f(X).
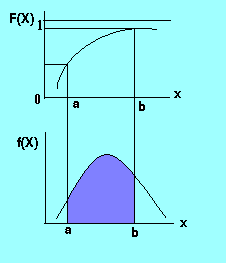
Значение F(b) равно вероятности события x<b. Разность F(b) - F(a) равна вероятности события a<x<b (вероятности попадания случайной величины в интервал (a,b)). При использовании функции f(x) вероятность попадания случайной величины в интервал (a,b) равно площади под кривой f(x) на этом интервале. Основное свойство непрерывной случайной величины - ВЕРОЯТНОСТЬ ТОГО, ЧТО НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА ПРИМЕТ КОНКРЕТНОЕ ЗНАЧЕНИЕ РАВНА НУЛЮ.
Графическое описание поведения дискретных случайных величин задается теми же функциями.
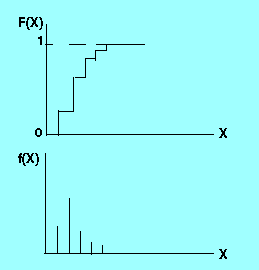
Табличное описание
случайных величин задается в виде таблиц. Для дискретной случайной величины
таблица имеет вид:
| X | x1 | x2 | x3 | ... | xn |
| P | p1 | p2 | p3 | ... | pn |
x1,
x2, x3,..., xn - значения дискретной случайной величины X
p1,
p2, p3,..., pn - вероятность P, с которой случайная величина принимает
соответствующие значения.
Для непрерывной случайной
величины таблица имеет вид:
|
X |
x1,x2 |
x2,x3 |
x3,x4 |
... |
xn-1,xn |
|
P |
p1 |
p2 |
p3 |
... |
pn |
x1,x2
x2,x3 x3,x4 ...
xn-1,xn - интервалы значений непрерывной случайной величины
X.
p1, p2, p3,...,
pn - вероятность, с которой
случайная величина попадает в соответствующий интервал.
Аналитическое описание случайных величин как правило
задается аналитическим описанием функции плотности распределения случайной
величины. Например, аналитическое описание нормального закона распределения
непрерывной случайной величины имеет вид:
f(x) = 1/[(D(x)*(2π)1/2]*exp[ -(x - M(x))2/(2*D(x)) ]
где x - случайная величина,
M(x),D(x) - параметры распределения,
exp[ ] - e в степени выражения в скобках