Идентификация модели стационарного временного ряда предназначена для предварительного определения типа модели (авторегрессия, скользящее среднее или смешанный процесс) и порядка модели (значения p и q). Однако автокорреляционная функция стационарного временного ряда не позволяет однозначно идентифицировать модель ряда. Это возможно с использованием второй дополнительной функции - частной автокорреляционной функции (ЧАКФ в русской транскрипции или PACF в английской транскрипции). Значения ЧАКФ - это значение m-го коэффициента в представлении временного ряда процессом авторегрессии порядка m. Пусть имеется стационарный временной ряд x(k). Рассмотрим следующие представления временного ряда через процесс авторегрессии:
x(k) - μ = a11*[x(k-1) - μ]
x(k) - μ = a12*[x(k-1) - μ] + a22*[x(k-2) - μ]
x(k) - μ = a13*[x(k-1) - μ] + a23*[x(k-2) - μ] + a33*[x(k-3) - μ]
... ... ... ... ... ... ... ... ...
x(k) - μ = a1*[x(k-1) - μ] + a2*[x(k-2) - μ] + a33*[x(k-3) - μ] + ... + amm*[x(k-m) - μ]
Значениями ЧАКФ для сдвигов 1, 2, 3, ..., m являются значения коэффициентов: a11, a22, a33, ..., amm. График ЧАКФ может иметь вид:
или
После оценивания ЧАКФ необходимо для каждого m проверить гипотезу о равенстве нулю соответствующего коэффициента частной автокорреляции. В программах статистической обработки данных для каждого из коэффициентов вычисляются критические значения, которые на графике оценки ЧАКФ приобретают вид контрольных границ. Например:
Согласно приведенному графику значимым является значение PACF(1). Ниже приведен пример ряда когда все значения PACF(m) для любого m>0 незначимы.
При идентификации модели как правило пользуются следующими правилами:
-
Если h первых значений АКФ отличны от нуля, а ЧАКФ по модулю асимптотически стремится к нулю, то имеет место процесс АРСС(0,h) - скользящего среднего порядка h.
-
Если h первых значений ЧАКФ отличны от нуля, а АКФ по модулю асимптотически стремится к нулю, то имеет место процесс АРСС(h,0) - авторегрессии порядка h.
-
Если значения АКФ и ЧАКФ по модулю асимптотически стремятся к нулю, то имеет место смешанный процесс АРСС(p,q).
Например, если соответствующие функции имеют вид:
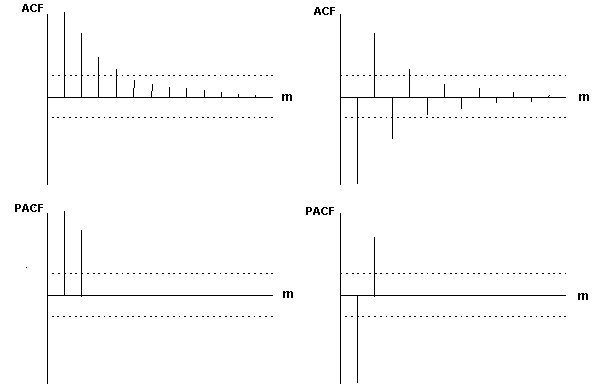
то имеет место процесс АРСС(2,0) - авторегрессии второго порядка.
Если функции имеют вид:
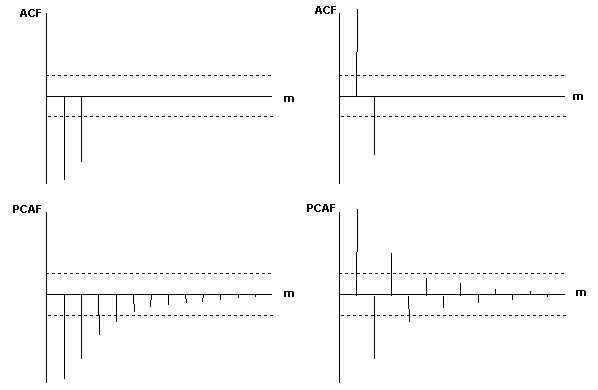
то временной ряд может быть представлен процессом АРСС(0,2) -скользящего среднего второго порядка.
Ниже представлены АКФ и ЧАКФ для одного из вариантов процесса АРСС(1,1) (характер функций зависит от знаков и значений коэффициентов)
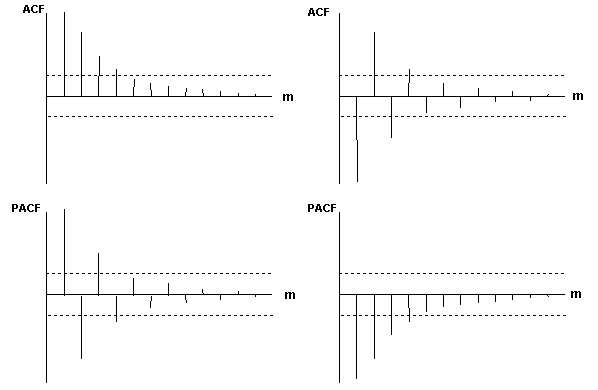
Этап идентификации модели временного ряда позволяет обосновать структуру модели и сократить трудозатраты на ее построение.