АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Оценивание параметров модели. Проверка адекватности модели
Оценивание параметров модели представляет особую задачу - модели могут быть нелинейными относительно параметров. В этой связи обычный метод наименьших квадратов здесь не применим. Оценивание осуществляется рекуррентными методами поиска экстремума (минимума суммы квадратов отклонений значений ряда от значений вычисляемых по модели). Поиск экстремума осуществляется по значениям оценок коэффициентов модели. Далее проверяется гипотеза о значимости коэффициентов. Незначимые коэффициенты удаляются из модели (приравниваются нулю). Однако, модель считается адекватной только в том случае, когда остаточные отклонения представляют собой непрогнозируемый временной ряд ("белый шум").
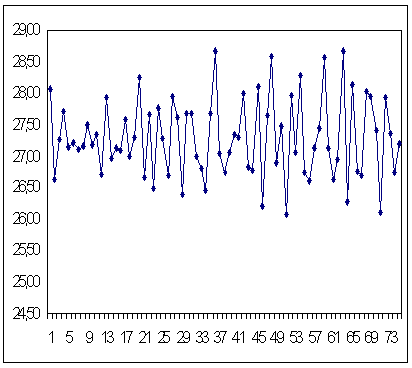
Рассмотрим пример. Ниже приведена реализация стационарного временного ряда.

Оценки АКФ и ЧАКФ ряда имеют вид:
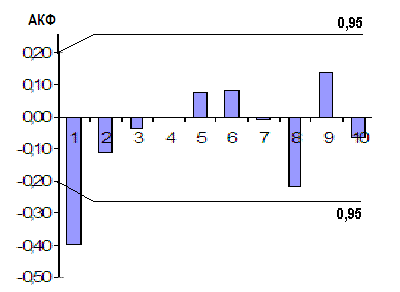
Используя приведенные функции, идентифицируем модель ряда как процесс скользящего среднего первого порядка: АРСС(0,1). Оценивание параметров модели средствами ППП "Statgraphics" приводит к следующему результату:
| Parameter | Estimate | Stnd. Error | t | P-value |
| MA(1) | 0,900766 | 0,0559425 | 16,1016 | 0,000000 |
| Mean | 27,2661 | 0,00656328 | 4154,33 | 0,000000 |
| Constant | 27,2661 |
При этом оценки АКФ и ЧАКФ остаточных отклонений от модели имеют вид:
Оценки АКФ и ЧАКФ остаточных отклонений показывают, что эти отклонения представляют собой непрогнозируемый временной ряд ("белый шум"). Таким образом, модель следует признать адекватной.
При рассмотрении моделей временных рядов указывалось, что если процесс скользящего среднего первого порядка представлять процессом авторегрессии, то теоретически порядок авторегрессии должен быть бесконечным. В нашем случае при представлении ряда авторегрессией мы получаем следующий результат оценивания параметров модели:
| Parameter | Estimate | Stnd. Error | t | P-value |
| AR(1) | -0,856472 | 0,114908 | -7,45357 | 0,000000 |
| AR(2) | -0,834394 | 0,142313 | -5,86308 | 0,000000 |
| AR(3) | -0,724958 | 0,150658 | -4,81193 | 0,000009 |
| AR(4) | -0,536149 | 0,141876 | -3,779 | 0,000331 |
| AR(5) | -0,273706 | 0,118208 | -2,31546 | 0,023567 |
| Mean | 27,2648 | 0,0132186 | 2062,62 | 0,000000 |
| Constant | 115,212 |
В этом случае необходимо оценивать 5 параметров (при задании более высокого порядка авторегрессии ППП "Statgraphics" принудительно переходит на представление скользящим средним первого порядка), вместо одного. Ниже представлен график прогноза по модели и доверительный интервал прогноза при доверительной вероятности 0,95.
Формула вычисления прогноза имеет вид:
x(k) = 27,2661 - 0,900766*[x(k-1) - x(k-1)]
где x(k) - прогноз по модели k-го значения временного ряда.
Проверьте усвоение Предыдущий раздел Следующий раздел Оглавление