МЕТОДЫ И ИНСТРУМЕНТАРИЙ МНОГОМЕРНОГО СТАТИСТИЧЕСКОГО АНАЛИЗА

Параметрическое описание многомерной случайной величины

При параметрическом описании поведение случайной величины определяется значениями специальных характеристик - параметров или моментов случайной величины. Напомним основные параметры описания одномерной случайной величины.

    Основной характеристикой является первый начальный момент, который называется МАТЕМАТИЧЕСКИМ ОЖИДАНИЕМ СЛУЧАЙНОЙ ВЕЛИЧИНЫ (МО):

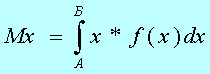
    где: Mx - значение математического ожидания случайной величины x;
   A,B - пределы интегрирования (A - минус бесконечность, B - плюс бесконечность);
   f(x) - функция плотности вероятности случайной величины x.
   Для дискретной случайной величины интеграл превращается в сумму. Математическое ожидание характеризует центр, относительно которого группируются значения случайной величины.

    Другими параметрами случайной величины являются ЦЕНТРАЛЬНЫЕ МОМЕНТЫ. Центральным моментом порядка k называется математическое ожидание отклонения значений случайной величины от центра в степени k:

    

R_k(x) = M[(x-Mx)^k],

    Доказано, что если функция плотности распределения случайной величины имеет одну вершину (функция унимодальна), то для полного описания поведения этой случайной величины достаточно указать МО и центральные моменты второго, третьего и четвертого порядка. Последние три характеристики имеют специальные названия.
   Второй центральный момент называется ДИСПЕРСИЕЙ: Dx = M[(x-Mx)²]. Дисперсия характеризует разброс значений случайной величины относительно МО. Обратите внимание, дисперсия всегда больше нуля.
   Третий центральный момент называется АСИММЕТРИЕЙ: Ax = M[(x-Mx)³]. Асимметрия характеризует "косость" графика функции плотности вероятности случайной величины. При Ax = 0 абсцисса вершины графика функции f(x) совпадает с МО (график симметричен). Если Ax < 0, то вершина этого графика расположена левее МО, при Ax > 0 вершина расположена правее МО.
   Четвертый центральный момент называется ЭКСЦЕССОМ: Ex = M[(x-Mx)⁴]. Этот момент характеризует "островершинность" графика f(x) и его значение всегда больше нуля.
   Наиболее распространенным в природе, а следовательно и наиболее часто применяемом для описания вероятностных процессов, является нормальный закон распределения. Для полного параметрического описания поведения случайной величины при нормальном законе распределения достаточно задания только двух параметров: математического ожидания и дисперсии. Асимметрия и эксцесс при нормальном законе распределения определяются через эти два параметра.

Пусть имеется случайный вектор X = (x₁,x₂, ... , x_k)^т , тогда математическое ожидание вектора MX = (Mx₁,Mx₂, ... , Mx_k)^т . Центральным смешанным моментом второго порядка  i-той и j-той компонент случайного вектора X называется ковариацией

cov(x_i,x_j) = M[(x_i - Mx_i)*(x_j - Mx_j)]

Многомерным аналогом ковариации является ковариационная матрица случайного вектора COV = M[(X - MX)(X - MX)^т], которая имеет вид:

 

D(x1)	cov(x1,x2)	...	cov(x1,xj)	...	cov(x1,xk)
cov(x2,x1)	D(x2)	...	cov(x2,xj)	...	cov(x2,xk)
...	...	...	...	...	...
cov(xi,x1)	cov(xi,x1)	...	D(xi)	...	cov(xi,xk)
...	...	...	...	...	...
cov(xk,x1)	cov(xk,x2)	...	cov(xk,xj)	...	D(xk)

Матрица симметрическая и неотрицательно определена.

---

Напоминание. Квадратная матрица A называется положительно определенной, если для любого ненулевого вектора X ≠ 0, X^тAX > 0. Аналогично определяются отрицательно (X^тAX < 0), неотрицательно (X^тAX ≥ 0) и неположительно (X^тAX ≤ 0) определенные матрицы.

---

Если элементы матрицы COV  нормировать, то получится корреляционная матрица R:

 

1	ρ(x1,x2)	...	ρ(x1,xj)	...	ρ(x1,xk)
ρ(x2,x1)	1	...	ρ(x2,xj)	...	ρ(x2,xk)
...	...	...	...	...	...
ρ(xi,x1)	ρ(xi,x1)	...	ρ(xi,xj)	...	ρ(xi,xk)
...	...	...	...	...	...
ρ(xk,x1)	cov(xk,x2)	...	ρ(xk,xj)	...	1

где ρ(x_i,x_j) = cov(x_i,x₁)/[D(x_i)*D(x_j)]^1/2 - коэффициент корреляции i-той и j-той компонент вектора X.

Очевидно, что матрица R так же как и матрица COV симметрическая и неотрицательно определена. Однако, эти матрицы при значениях k > 2 не позволяют полностью описать связи между компонентами вектора X. Зависимость между компонентом x_i и остальными компонентами x₁, x₂, ...x_i-1, x_i+1, ..., x_k можно представить в виде:

x_i = z_i(x₁, x₂, ...x_i-1, x_i+1, ..., x_k) + e_i(x₁, x₂, ...x_i, ..., x_k),

где z_i(x₁, x₂, ...x_i-1, x_i+1, ..., x_k) - некоторая функция k-1 компонент вектора X,

        e_i(x₁, x₂, ...x_i, ..., x_k) - остаточные отклонения.

Функция z_i(x₁, x₂, ...x_i-1, x_i+1, ..., x_k) называется регрессией компонента x_i на компоненты x₁, x₂, ...x_i-1, x_i+1, ..., x_k. В большинстве исследований в качестве регрессии выбирают функцию минимизирующую математическое ожидание квадрата отклонений M[(x_i - e_i)²]. Можно показать, что минимум достигается когда z_i(x₁, x₂, ...x_i-1, x_i+1, ..., x_k) равно условному математическому ожиданию M(x_i/x₁, x₂, ...x_i-1, x_i+1, ..., x_k).

Показателем, характеризующим рассеяние случайной величины x_i при фиксированных x₁,x₂,...,x_i-1, x_i+1, ..., x_k является условная дисперсия

D(x_i/x₁, x₂, ...x_i-1, x_i+1, ..., x_k)=M[x_i - M(x_i/x₁, x₂, ...x_i-1, x_i+1, ..., x_k)]²

Эта дисперсия называется остаточной D_{ост i} . Тогда отношение этой дисперсии к дисперсии компоненты i называется корреляционным отношением:

1 - η_i² =   D_{ост i}/D(x_i)

или

η_i² = 1 - D_{ост i}/D(x_i)

Корреляционное отношение показывает какая доля общего рассеяния случайных величин x₁, ..., x_k обусловлена рассеянием случайной величины x_i.

Показателем меры линейной зависимости x_i от x₁, x₂, ...x_i-1, x_i+1, ..., x_k служит множественный коэффициент корреляции R_i0 :

R_i0 = (1 - |R|/|R_ii|)^1/2

где |R| - определитель корреляционной матрицы;

    |R_ii| - определитель минора матрицы R, получаемого вычеркиванием j-той строки и j-того столбца.

Если зависимость x_i от x₁, x₂, ...x_i-1, x_i+1, ..., x_k линейна, то справедливо равенство:

R²_i0 = η_i²

Представленные параметры позволяют описать поведение случайного вектора X, если компоненты вектора распределены по нормальному закону.

Непрерывная k-мерная случайная величина распределена нормально, если плотность распределения имеет вид:

f(X)=[ (2π)^k |COV| ]^-1/2 exp[ -(X-MX)^т(COV)^-1(X-MX)/2 ],

где: MX = (Mx₁,Mx₂, ... , Mx_k)^т - математическое ожидание вектора X,

        (COV)^-1 - матрица обратная ковариационной матрице COV,

        |COV| - определитель ковариационной матрицы.

Если k=2, то введя обозначения:

D(x₁)=σ₁², D(x₂)=σ₂², Mx₁=µ₁, Mx₂=µ₂, ρ(x₁,x₂)=ρ

то функция плотности вероятности двумерного нормального распределения имеет вид:

 f(X)=[ (2π)σ₁σ₂(1 - ρ²)^1/2 ]^-1 exp[ -Q(x₁,x₂)/2 ],

где:

Q(x₁,x₂)=[(x₁-µ₁)²/σ₁² - 2ρ(x₁-µ₁)²(x₂-µ₂)²/(σ₁σ₂) + (x₂-µ₂)²/σ₂²]

Таким образом в скалярных параметрах двумерное нормальное распределение требует для своего описания пять параметров: два математических ожидания (µ₁, µ₂), две дисперсии: (σ₁², σ₂²) и коэффициент корреляции ρ.

Проверьте усвоение  Предыдущий раздел  Следующий раздел  Оглавление