МНОЖЕСТВЕННЫЙ РЕГРЕССИОННЫЙ
АНАЛИЗ. МЕТОД ГЛАВНЫХ КОМПОНЕНТ
Метод главных компонент
Метод главных
компонент (МГК) применяется для снижения размерности пространства наблюдаемых
векторов, не приводя к существенной потере информативности.
Предпосылкой МГК является нормальный закон распределения многомерных векторов. В
МГК линейные комбинации случайных величин определяются характеристическими
векторами ковариационной матрицы. Главные компоненты представляют собой
ортогональную систему координат, в которой дисперсии компонент характеризуют их
статистические свойства.
Пусть дан исходный
набор векторов X линейного пространства Lk.
Применение метода главных компонент позволяет перейти к базису пространства
Lm (m≤k), такому что: первая компонента (первый
вектор базиса) соответствует направлению, вдоль которого дисперсия векторов
исходного набора максимальна. Направление второй компоненты
(второго вектора базиса) выбрано таким образом, чтобы дисперсия исходных
векторов вдоль него была максимальной при условии ортогональности первому
вектору базиса. Аналогично определяются остальные векторы базиса. В результате,
направления векторов базиса выбраны так, чтобы максимизировать дисперсию
исходного набора вдоль первых компонент, называемых главными компонентами (или
главными осями). Получается, что основная изменчивость векторов исходного набора
векторов представлена несколькими первыми компонентами, и появляется
возможность, отбросив оставшиеся (менее существенные) компоненты, перейти к
пространству меньшей размерности.
Результатом применения МГК является вычисление матрицы W размера
m*k, осуществляющей проекцию векторов пространства
Lk на подпространство, натянутое на главные компоненты:
Y = W*(X - μ),
Y ∈ Lm, X ∈
Lk.
Где X - вектор из исходного набора,
Y -
координаты вектора в подпространстве главных компонент, μ -
математическое ожидание вектора
X начального набора.
Главные компоненты
(векторы базиса), выбираемые с помощью МГК, обладают следующим свойством:
обратная проекция вектора Y в Lk дает
минимальную ошибку реконструкции (минимальное расстояние до образа вектора
Y). Нужно отметить, что корректное применение МГК возможно лишь при
предположении о нормальном распределении векторов исходного набора.
Пусть имеется реализация (20 наблюдений) двумерного вектора
X. На рисунке

представлена совокупность наблюдений. Определение главных
компонент Y вектора X
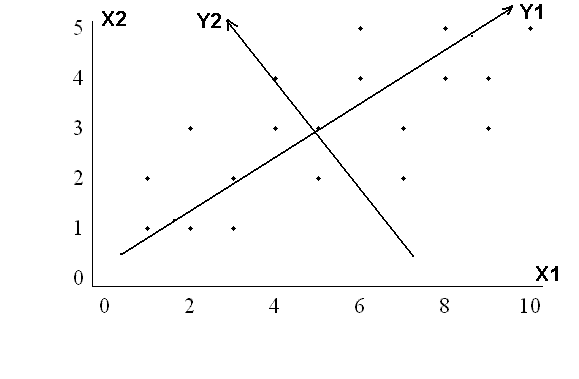
состоит в определении новых осей координат по условию:
направление координаты y1
должно соответствовать максимальному рассеянию наблюдений, направление
y2 должно соответствовать
направлению с максимальном рассеянием наблюдений среди всех
направлений
ортогональных y1. Если исходные
данные нормировать, то начало координат главных компонент будет соответствовать
X = (x1,x2)т
, дисперсии компонент, будут равны единице.
Решение задачи методом главных компонент сводится
к поэтапному преобразованию матрицы исходных данных X.
Пусть X –
матрица
исходных данных размерностью
n*k (n – число объектов
наблюдения, k
– число элементарных аналитических
признаков),
тогда
Z
– матрица центрированных и нормированных
значений признаков, элементы матрицы вычисляют по формуле:
zi,j =( xi,j -
xj )/Sj,
где:
xi,j
- i-ое значение j-ой
компоненты вектора X,
i=1,2, ... ,n; j=1,2, ... ,k,
xj -
оценка математического ожидания j-ой
компоненты вектора X:
xj
=∑i
xi,j/n
,
Sj - корень
квадратный из оценки дисперсии j-ой
компоненты вектора X:
S2j
=
∑i
(xi,j -
xj
)2/(n-1).
Матрица оценок парных корреляций
R
вычисляется по формуле:
R=(Zт*Z)/(n-1).
Напомним, что оценка ковариационной матрицы
C
вычисляется по формуле:
C =
(Xт*X)/(n-1).
Далее вычисляется диагональная матрица Λ
собственных
(характеристических) чисел.
Напоминание
Пусть A — квадратная матрица. Вектор
V
называется собственным вектором матрицы A если
A*V = λ*V, где число λ называется
собственным значением матрицы A. Таким образом
преобразование, которое выполняет матрица A над вектором
V, сводится к простому растяжению или сжатию с коэффициентом
λ. Собственный вектор определяется с точностью до умножения на константу
α ≠ 0, т.е. если V — собственный вектор, то и αV
— тоже собственный вектор.
У матрицы A , размерностью (n*n) не может быть больше
чем n собственных значений. Они
удовлетворяют характеристическому уравнению det(A
− λI) = 0, являющемуся алгебраическим уравнением
n-го порядка. Набор собственных значений
λ1,..., λn
матрицы A называется спектром A.
Спектр обладает разнообразными свойствами. В частности det(A)
= λ1×...×λn, Sp(A)
= λ1+...+λn.
Собственные значения произвольной матрицы могут быть комплексными числами,
однако если матрица симметричная (Aт
= A), то ее собственные значения вещественны.
Пусть имеется матрица A:
тогда
det(A − λI)
= (1 -
λ)*(3
- λ) - 2*4 = λ2 -
4*λ
- 5 = 0
λ1
= 5,
λ2
= -1; det(A) =
λ1*λ2
= 5*(-1) = -5; Sp(A) = λ1
+ λ2 = 5 - 1 = 4
Cобственные вектора:
V1
=
(0,7,
0,7)т и
V2 = (0,89,
-0,45)т
A*V1
=
λ1*V1
= (3,5, 3,5)т
= 5*(0,7,
0,7)т ;
A*V2
=
λ2*V2
= (-0,89, 0,45)т
= -1*(0,89,
-0,45)т
Квадратную (в частности симметричную) матрицу A можно привести
к диагональному виду преобразованием подобия A = ΛT−1
Здесь Λ = diag(λ1,...,
λn) — это диагональная матрица, элементами которой являются
собственные значения матрицы A, а T — это
матрица, составленная из соответствующих собственных векторов матрицы A,
т.е. T = (V1,...,Vn).
Множество решений
λj
находят решением характеристического
уравнения |R - λI| =
0.
Характеристики вариации λj
- показатели
оценок дисперсий каждой главной компоненты. Суммарное значение Σλj
равно сумме оценок дисперсий элементарных
признаков xj.
При условии стандартизации исходных данных, эта сумма равна числу элементарных
признаков k.
Решив характеристическое уравнение, находят его
корни λj.
После этого вычисляют собственные векторы
матрицы
R.
Реально это означает решение
k
систем линейных уравнений для каждого
при j = 1, ..., k. В общем виде система
имеет вид:
(1-λj
)*v1j + r12*v2j +r13*v3j
+ ... +r1k*vkj = 0,
r21*v1j +
(1-λj
)*v2j
+r23*v3j + ... +r2k*vkj = 0,
...............................................................................
rk1*v1j + rk2*v2j +rk3*v3j
+ ... +(1-λj
)*vkj
= 0,
Приведенная система объединяет однородные
линейные уравнения, и так как число ее уравнений равно числу неизвестных, она
имеет бесконечное множество решений. Конкретные значения собственных векторов
при этом можно найти, задавая произвольно по крайней мере величину одной
компоненты каждого вектора.
Далее вычисляется матрица
A
– матрица компонентного отображения, ее
элементы akj –
весовые коэффициенты. Вначале
A имеет размерность
k*k
– по числу элементарных признаков
Xj,
затем в анализе остается
m
наиболее значимых компонент,
m ≤ k.
Вычисляют матрицу
A
по известным данным матрицы собственных
чисел Λ и нормированных собственных векторов
V
по формуле A = V*Λ1/2.
G
– матрица значений главных компонент
размерностью k*n,
G = A-1Zт
. Эта матрица в общем виде записывается:
| g11 |
g12 |
... |
g1n |
|
g21 |
g22 |
... |
g2n |
| ... |
... |
... |
... |
|
gk1 |
gk1 |
... |
gkn |
Эта матрица показывает значения всего набора главных
компонент (число главных компонент равно k).
При снижении размерности до m главных компонент
размер матрицы будет m*n. Величина
m либо назначается пользователем, либо
определяется по значениям
λj.
Например, в ППП
"Statgraphics" по умолчанию остаются только те главные
компоненты, собственные числа которых не меньше единицы.
Проверьте усвоение
Предыдущий раздел
Следующий раздел
Оглавление